Introduction
The Learning from Demonstration (LfD) paradigm provides a powerful framework for learning policies that are capable of executing complex motions.
In spite of the success of this paradigm, the issue of compounding errors remains a key challenge and existing approaches that seek
to address this problem such as collecting more data with/without human supervision, action chunking, temporally ensembling predictions or directly learning dynamical systems with convergence guarantees
each come with significant tradeoffs. Motivated by this challenge we sought to design a neural network layer that could be incorporated into existing neural network architectures
while addressing the issue of compounding errors and avoiding the overhead encountered in existing approaches.
To accomplish this goal we turn our attention to Reservoir Computing, a computational paradigm which has traditionally been used to accurately model complex dynamical systems.
In particular, we focused our attention on Echo State Networks (ESNs) and their ability to model complex temporal dynamics. This inspired us to design a dynamical system which
satisfied the Echo State Property that is present in ESNs but that could also be readily incorporated into existing neural network architectures.
The result of this goal is the neural network layer introduced in our paper and summarised in the next section. In order to validate our proposed neural network layer, we evaluated it on the task
of reproducing human handwriting motions using the LASA Human Handwriting Dataset. Below we show the qualitative results of our model against
(a) a standard ESN, (b) a feedforward neural network that is identical to ours except it omits our neural network layer and (c) the same feedforward model with temporal ensembling applied to its predictions.
As shown below, our method maintains a high degree of precision while also maintaining low latency for the drawing task.
Example rollouts of policies trained on the S character drawing task. In each plot the model prediction is progressively overlayed on top of the expert demonstration.
The area between the expert demonstration and model prediction is used to highlight the differences in precision between the various approaches, while the overall speed
of the drawing task reflects the latency of each model.
Method Overview
The neural network layer we introduce is unlike traditional neural network layers in which parameters are learnable and trained via backpropagation. In contrast,
we optimise the structure of a dynamical system model with properties that result in representations which are useful for learning. In particular, in this work
we focus on designing a dynamical system with the Echo State Property. We start by introducing this property and how we
design a neural network layer with this property.
The Echo State Property
The echo state property defines the asymptotic behaviour of a dynamical system with respect to the inputs driving the system.
Given a discrete-time dynamical system $\mathcal{F}: X \times U \rightarrow X$, defined on compact sets $X, U$ where $X \subset \mathbb{R}^{N}$
denotes the state of the system and $U \subset \mathbb{R}^{M}$ the inputs driving the system; the echo state property is satisfied if the following conditions hold:
$$
\begin{split}
& x_{k} = F(x_{k-1}, u_{k}), \\
& \forall u^{+\infty} \in U^{+\infty},~ x^{+\infty} \in X^{+\infty},~ y^{+\infty} \in X^{+\infty},~ k \geq 0, \\
& \exists (\delta_{k})_{k\geq0} : || x_{k} - y_{k} || \leq \delta_{k}.
\end{split}
$$
where $(\delta_{k})_{k \geq 0}$ denotes a null sequence, each $x^{+\infty}, y^{+\infty}$ are compatible with a given $u^{+\infty}$ and right infinite sets are defined as:
$$
\begin{split}
& U^{+\infty} := \{u^{+\infty} = (u_{1}, u_{2},...) | u_{k} \in U ~ \forall k \geq 1\} \\
& X^{+\infty} := \{x^{+\infty} = (x_{0}, x_{1},...) | x_{k} \in X ~ \forall k \geq 0\} \\
\end{split}
$$
These conditions ensure that the state of the dynamical system is asymptotically driven by the sequence of inputs to the system.
This is made clear by the fact that the conditions make no assumptions on the initial state of trajectories, just that they must be compatible with the driving inputs and asymptotically converge to the same state.
This dynamical system property is especially useful for learning representations for dynamic behaviours as the current state of the dynamical system (embeddings when incorporated into a neural network architecture)
is driven by the control history.
Constructing our Dynamical System
The construction of our neural network layer is very similar to the construction of an ESN with the key difference being that our dynamics incorporate learnt embeddings.
The discrete time dynamical system is constructed through the following steps:
1. Sample connections of an adjacency matrix for a graph that represents the dynamical system.
2. Sample weights of connections to create a weighted adjacency matrix.
3. Compute the spectral radius of the resulting weighted adjacency matrix.
4. Scale matrix such that the spectral radius is now less than one.
5. Sample fixed set of weights for input mapping of data.
Sampling the weights for the graph representing the dynamics is outlined more formally below:
$$
\begin{split}
&A_{ij} =
\begin{cases}
1 & \text{with probability } 0.01 \\
0 & \text{with probability } 0.99
\end{cases} \\ \\
&W_{ij} =
\begin{cases}
w_{ij} & \text{if } A_{ij} = 1, w_{ij} \sim \mathbb{U}[-1, 1] \\
0 & \text{if } A_{ij} = 0
\end{cases}\\ \\
&\rho(W) := \max \left\{ |\lambda_i| : \lambda_i \text{ is an eigenvalue of } W \right\} \\ \\
&W_{\text{dynamics}} = \frac{WS}{\rho(W)}
\end{split}
$$
The fixed input weights are sampled uniformly as follows where parameter $a$ defines the bounds of the sampling procedure:
$$
\begin{split}
&W_{\text{in}} \sim \mathbb{U}[-a, a]
\end{split}
$$
Given the parameters representing the dynamics model $W_{\text{dynamics}}, W_{\text{in}}$ along with neural network $f_{\theta_{\text{in}}}$ and input data $u$ and task conditioning data $\mathcal{T}$
we construct the following forward dynamics equations:
$$
\begin{split}
&I(t) := W_{\text{in}}u(t) + f_{\theta_{\text{in}}}(u(t), \mathcal{T}) \\
&\tilde{x}(t) := tanh(I(t) + W_{\text{dynamics}}x(t-1)) \\
&x(t) := (1 - \alpha)x(t-1) + \alpha\tilde{x}(t)
\end{split}
$$
where $\alpha$ is a tunable hyperparameter known as the leak rate, $I$ is the combination of fixed and learnt input mappings, $\tilde{x}$ state update term and $x$ dynamical system state.
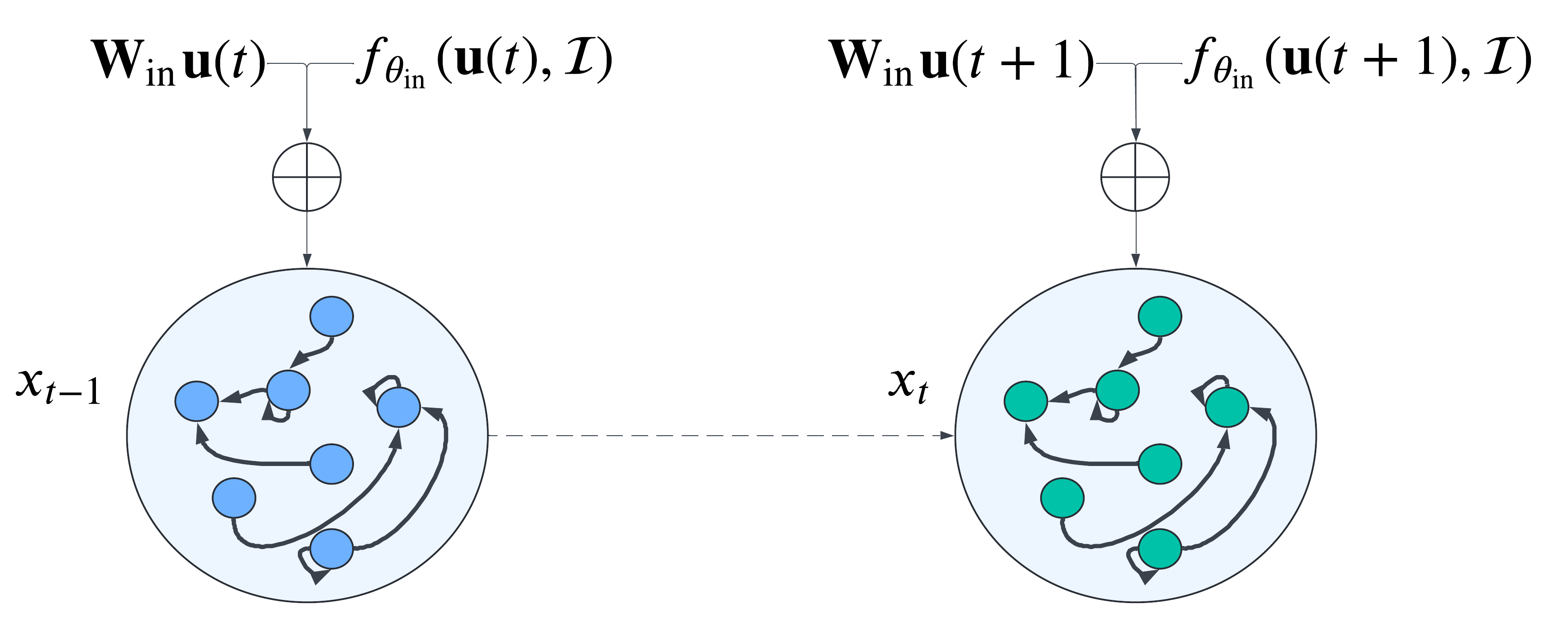
A representation of performing forward dynamics to update the state of our dynamical system model from one timestep to the next.
Importantly our dynamics incorporate both fixed and learnable embeddings.
Incorporation into Neural Network Architectures
Incorporating our layer into a larger neural network architecture enables us to benefit from the generalisation capabilities of existing
neural network components such as the attention mechanism. When incorporating our layer into an architecture, preceeding neural network layers
are considered as the learnt input mapping $f_{\theta_{\text{in}}}$ while a fixed mapping $W_{\text{in}}$ of the input data $u$ must also be provided to our neural network layer.
The outputs from our layer are high-dimensional embeddings constructed from the state $x$ of the dynamical system. An example for the multi-task
variant of a model incorporating our layer is provided below:
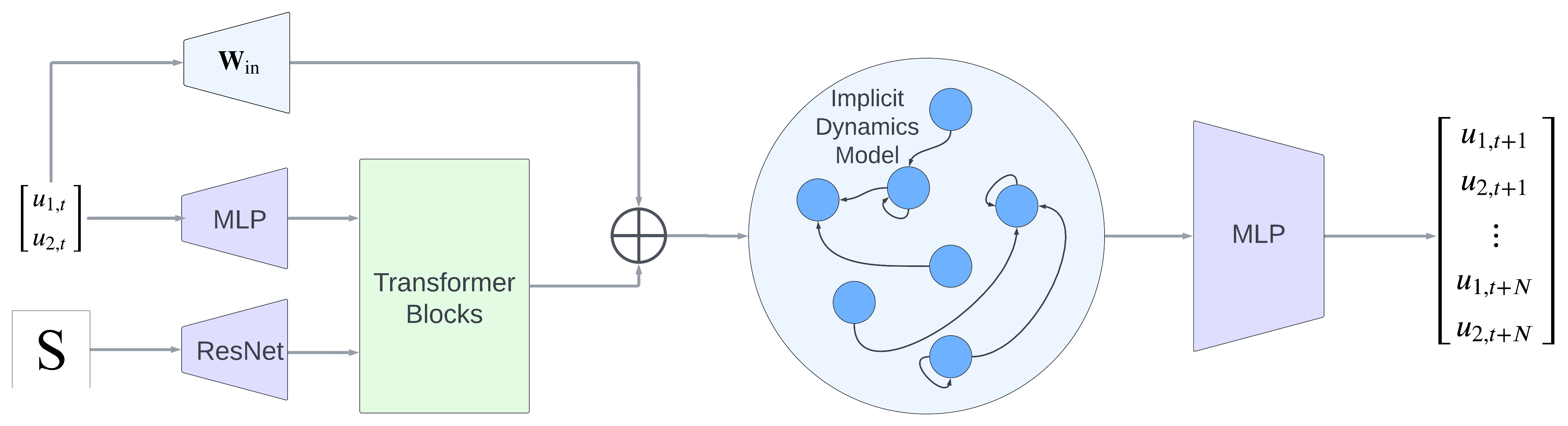
High-level schematic of the multi-task feedforward architecture that incorporates our dynamics model layer.
Experiments
Spatial Precision
Our experiments evaluate models for both the single and multi task setting of generating handwritten characters. In order to assess the ability of each model to fit the spatial characteristics of the expert
demonstrations we report the Fréchet distance along with the length of time it took to complete the character drawing. Metrics for the single task setting are provided below:
| Model |
S - Fréchet Distance |
S - Drawing Latency (MS) |
C - Fréchet Distance |
C - Drawing Latency (MS) |
L - Fréchet Distance |
L - Drawing Latency (MS) |
| Ours |
2.38 |
3.75 |
1.7 |
3.65 |
1.69 |
3.63 |
| ESN |
4.08 |
4.02 |
3.28 |
3.4 |
1.73 |
3.18 |
| FF |
3.7 |
3.4 |
3.2 |
3.68 |
2.68 |
3.81 |
| FF_Ensemble |
5.02 |
7.21 |
2.92 |
7.02 |
2.4 |
7.06 |
The multi task setting results are provided below:
| Model |
Fréchet Distance |
Drawing Latency (MS) |
| Ours |
4.19 |
13.88 |
| ESN |
10.52 |
10.64 |
| FF |
4.62 |
14.16 |
| FF_Ensemble |
4.93 |
25.7 |
As is evident in both sets of results, our model achieves the lowest Fréchet distance and is hence able to more closely fit the spatial characteristics of the expert demonstration data in both the single and multi task setting.
Qualitative results for drawing characters using a single multitask model.
Robustness to Perturbation
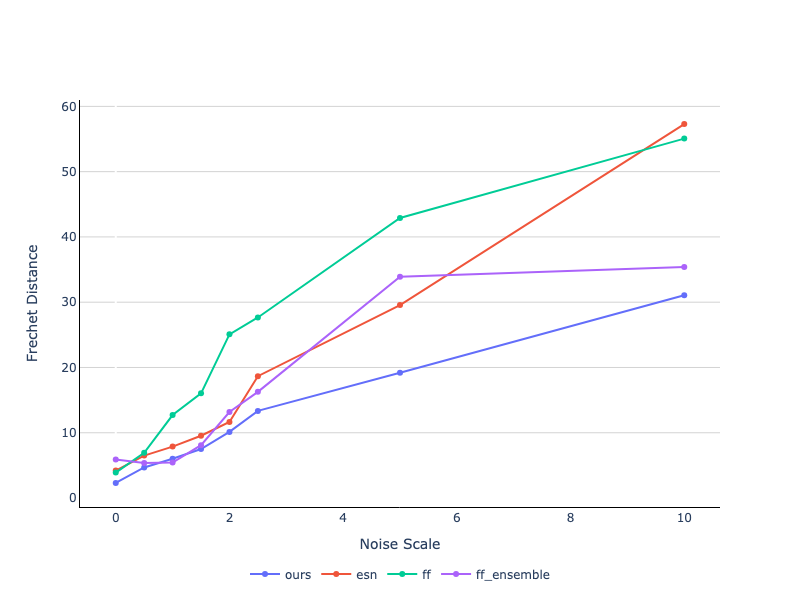
We assess the ability of various models to remain robust to noise by adding noise sampled from a standard Gaussian where we scale the
variance of the gaussian by the noise scale parameter. Below we plot the Fréchet distance by noise scale finding that our model remains
robust with increasing levels of noise, followed by the temporal ensemble of the feedforward architecture.
Jerk of Motions
The jerk or rate of change of acceleration that is associated to the predicted trajectory is of great practical importance in real world applications such as robotics.
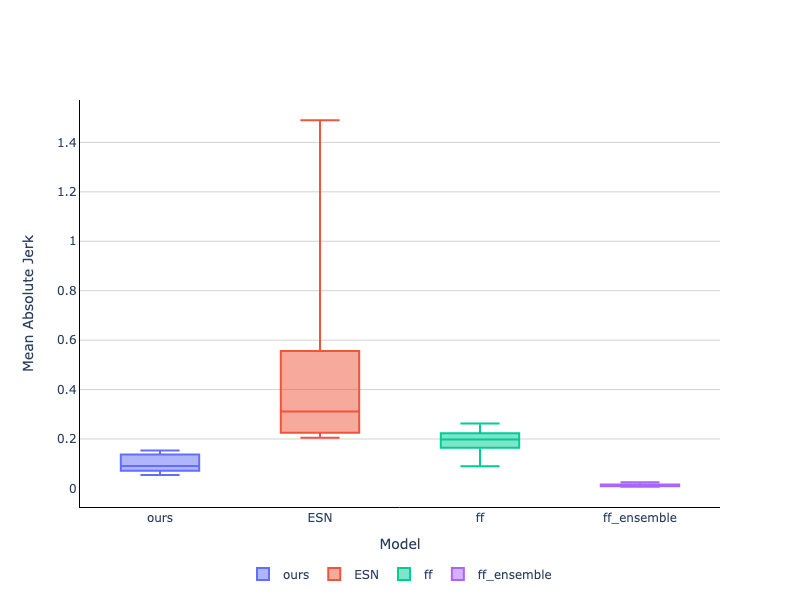
In this section, we look at the distribution of the mean absolute jerk squared across various policy rollouts. We find that temporally ensembling parameters leads to
the lowest amount of jerk but this also drastically reduces the speed at which the motion is executed, our model's distribution of jerk is the second lowest and relatively tight
indicating the ability of our model to generate smooth motions without the penalty of reducing the speed of execution.
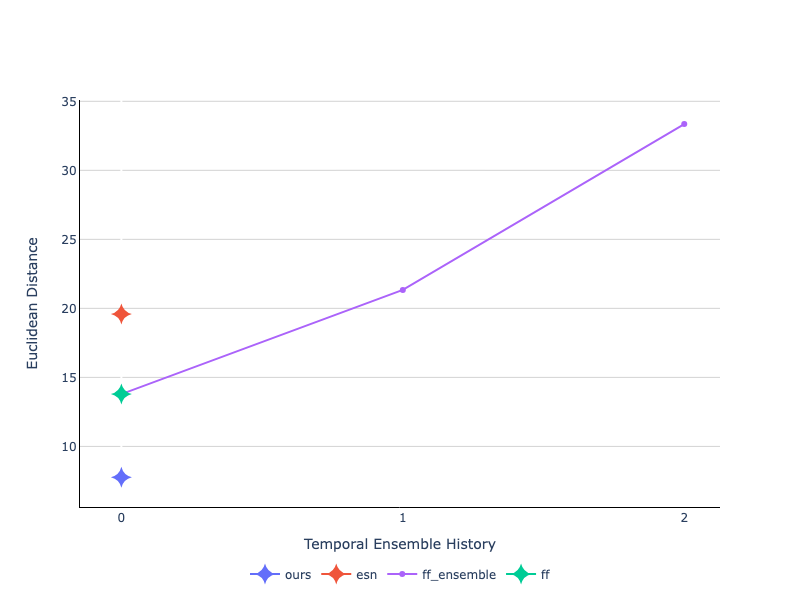
Velocity Profile Similarity
In this section, we look at how well the velocity profile of motions correspond to the expert demonstration. This is accomplished through applying
Dynamic Time Warping (DTW) to the predicted and demonstrated trajectory and subsequently computing the absolute euclidean distance.
We find that our method most faithfully represents the velocity profile of expert demonstrations. We also find that increasing the prediction horizon
over which temporal ensembles are performed results in more dissimilar velocity profiles.
Discussion and Future Work
In this work we introduced a new neural network layer that takes inspiration from existing literature on Echo State Networks. We demonstrate that the
layer can lead to improved performance in learning from demonstration on human handwriting traces. In particular, we show that the layer results in
a better alignment between the spatial and velocity characteristics of the predicted and demonstrated trajectories. We also
demonstrate that the layer leads to benefits in terms of robustness to perturbations. Furthermore, we incorporate the layer into a multitask model that
leverages a number of transformer blocks as a backbone resulting in the generalisation of our results to the multitask setting.
A key limitation which we did not address in this report is the handling of stopping conditions and model convergence. Furthermore, we did not evaluate
the layer we introduced in real world learning from demonstration tasks such as those in robotics. These are areas we aim to address in future work.
Finally, we introduced what to our knowledge is a novel paradigm for the design of neural networks architectures. Here we design properties of a dynmical system
and fix its parameters before incorporating it into a neural network architecture. We believe that this direction holds a lot of promise in tasks that require
some form of temporal modelling and we are motivated to study the design of useful dynamical system properties for learning. If this direction also interests you
especially from the standpoint of learning from demonstration in robotics please reach out as we are open to collaborations.
Citation
@article{placeholder,
title={Learning from Demonstration with Implicit Nonlinear Dynamics Models},
author={Peter David Fagan},
journal={Placeholder},
year={2024}
}














